Big O is a massive topic that took me no time at all to understand the basics, but understanding the more complex intricacies of this notation caused me some issues. Today I will be going through the basics in preparation of part 2, which will cover more advanced scenarios.

Big O

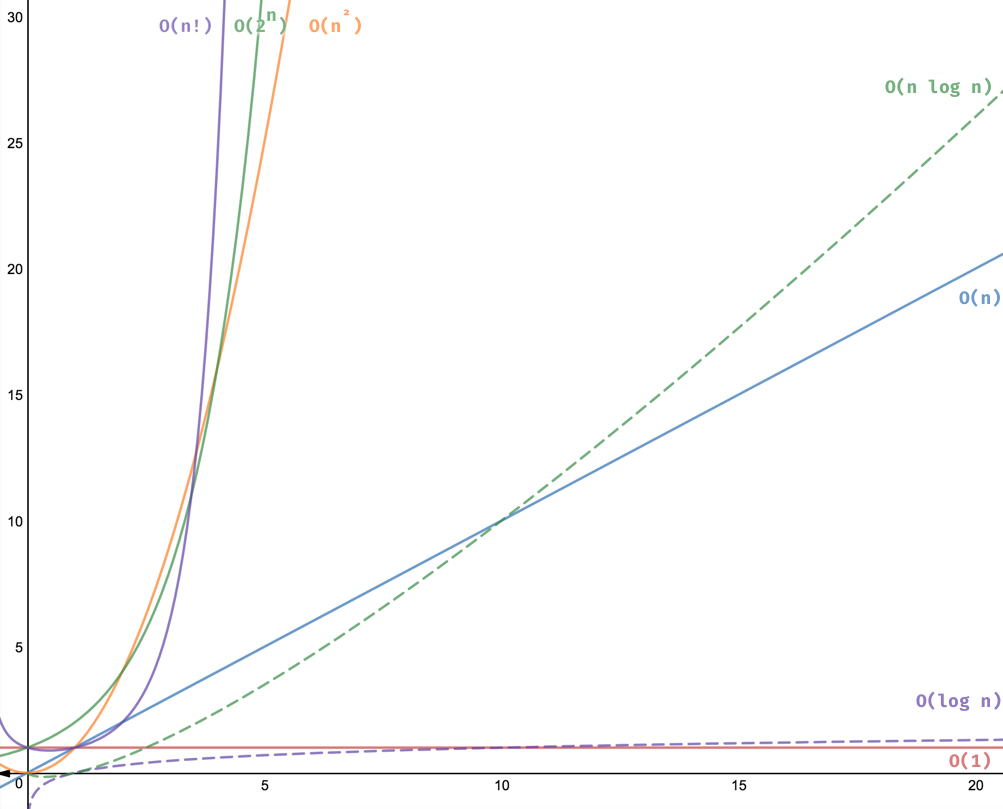
Big O is the metric used to define space and time complexity of an algorithm, and how the algorithm scales. On small data sets, these complexities may not matter too much. But if we have data set that is 1TB? All of a sudden, the computational time and space requirements become important. Not only for the processing speed, but for the amount of resources used to process and store this data.

In mathematics:

• O (big O) specifically defines the upper bound on time
• Ω (big Omega) defines the lower bound
• Θ (bit theta) defines both, giving us a tight bound on time.

However, in computing, Θ and O have been kind of merged, and O is now essentially Θ. However, it is worth knowing the mathematical differences. You shoudl note that we tend to not measure the best case time complexity of an algorithm, as generally there is no point. Data very rarely comes to us in an optimised way. What we care about is the worst case scenario for both time and space complexity.

Space complexity uses the same notation as time complexity. But instead of notating the processing time, we are calculating the worst case for the amount of resources the execution of our algorithm will take up. Do we need to create a single array (O(n))? Do we need to create a multidimensional array(O(N^2))? Is the function recursive? If it is we need to add each recursive call to the call stack etc.

The key is to know what is important information and what isn’t. Consider the fact that for a given set of inputs, O(n) may actually run faster than O(1), which means that we can drop any constants from our complexity. Also, as we are trying to understand worse case scenarios, we can drop any non-dominant terms. For example, if you work out the complexity of an algorithm is O(N^2 + N), N is not very important, so we drop it. Making the complexity O(N^2).

Rate of increase for common big O times